Aljabar adalah salah satu cabang penting dalam matematika. Kata aljabar berasal dari kata al-jabr yang diambil dari buku karangan Muhammad Ibn Musa Al-Khwarizi (780-
850 M),yaitu kitab al-jabr wa al-nuqabalah yang membahas tentang cara menyelesaikan persamaan-persamaan aljabar. Pemakaian aljabar ini sebagai penghormatan kepada Al- Khwarizi atas jasa-jasanya dalam mengembangkan aljabar melalui karya-karya tulisnya.
A . Unsur-Unsur Aljabar
1. Variabel
Variabel adalah lambang pengganti suatu bilangan yang belum diketahui nilainya dengan jelas. Variabel disebut juga peubah. Variabel biasanya dilambangkan dengan huruf kecil a, b, c, ... z.
Contoh:
Suatu bilangan jika dikalikan 5 kemudian dikurangi 3, hasilnya adalah 12. Buatlah bentuk persamaannya!
Jawab:
Misalkan bilangan tersebut x, berarti 5x – 3 = 12. (x
2. Konstanta
Suku dari suatu bentuk aljabar yang berupa bilangan dan tidak memuat variabel disebut konstanta.
Contoh:
Tentukan konstanta pada bentuk aljabar berikut. a. 2x2 + 3xy + 7x – y – 8
Jawab:
a. Konstanta adalah suku yang tidak memuat variabel, sehingga konstanta dari
2 x2 + 3xy + 7x – y – 8 adalah –8
3. Koefisien
Koefisien pada bentuk aljabar adalah faktor konstanta dari suatu suku pada bentuk aljabar.
Contoh:
Tentukan koefisien x pada bentuk aljabar berikut.
a. 5 x2y + 3x
Jawab:
a. Koefisien x dari 5 x2y + 3x adalah 3.
4. Suku
Suku adalah variabel beserta koefisiennya atau konstanta pada bentuk aljabar yang dipisahkan oleh operasi jumlah atau selisih.
a. Suku satu adalah bentuk aljabar yang tidak dihubungkan oleh operasi jumlah atau selisih.
Contoh: 3x, 4 a2, –2ab,
b. Suku dua adalah bentuk aljabar yang dihubungkan oleh satu operasi jumlah atau selisih.
Contoh: a2+ 2, x + 2y, 3 x2 – 5x,
c. Suku tiga adalah bentuk aljabar yang dihubungkan oleh dua operasi jumlah atau selisih.
Contoh: 3 x2 + 4x – 5, 2x + 2y – xy,
Bentuk aljabar yang mempunyai lebih dari dua suku disebut suku banyak atau polinom.
B. OPERASI ALJABAR
1. Penjumlahan dan Pengurangan Bentuk Aljabar
Pada bagian ini, kamu akan mempelajari cara menjumlahkan dan mengurangkan suku-suku sejenis pada bentuk aljabar. Pada dasarnya, sifat- sifat penjumlahan dan pengurangan yang berlaku pada bilangan riil, berlaku juga untuk penjumlahan dan pengurangan pada bentuk-bentuk aljabar, sebagai berikut.
a. Sifat Komutatif
a + b = b + a, dengan a dan b bilangan riil
b. Sifat Asosiatif
(a + b) + c = a + (b +c), dengan a, b, dan c bilangan riil
c. Sifat Distributif
a (b + c) = ab + ac, dengan a, b, dan c bilangan rii.
Contoh Soal :
1. Sederhanakan bentuk aljabar berikut :
1.) 3ab+5ab=
2.) 12y+7+3y+2=
3.) 5p-6p2-4p+9p2=
Penyelesaian :
1.) 3ab+5ab =8ab
2.) 12y+7+3y+2 = (12y+3y)+(7+2)
= 15y+9
3.) 5p-6p2-4p+9p2 = (-6p2+9p2)+(5p-4p)
= 3p2+p
2. Perkalian Bentuk Aljabar
Perhatikan kembali sifat distributif pada bentuk aljabar. Sifat distributif merupakan konsep dasar perkalian pada bentuk aljabar. Untuk lebih jelasnya, pelajari uraian berikut.
A . Perkalian Suku Satu dengan Suku Dua
Agar kamu memahami perkalian suku satu dengan suku dua bentuk aljabar, pelajari contoh soal berikut.
Contoh Soal :
Gunakan hukum distributif untuk menyelesaikan perkalian berikut.
a. 2(x + 3)
b. –5(9 – y)
Penyelesaian :
a. 2(x + 3) = 2x + 6
b. –5(9 – y) = –45 + 5y
B. Perkalian Suku Dua dengan Suku Dua
Agar kamu memahami materi perkalian suku dua dengan suku dua bentuk aljabar, pelajari contoh soal berikut.
Contoh Soal :
Tentukan hasil perkalian suku dua berikut, kemudian sederhanakan.
a. (x + 5)(x + 3)
b. (x – 4)(x + 1)
Penyelesaian :
a. (x + 5)(x + 3) = (x + 5)x + (x + 5)3
= x2 + 5x + 3x + 15
= x2 + 8x + 15
b. (x – 4)(x + 1) = (x – 4)x + (x – 4)1
= x2 – 4x + x – 4
= x2 – 3x – 4
Amati kembali Contoh Soal. Ternyata perkalian dua suku bentuk aljabar (a + b) dan (c + d) dapat ditulis sebagai berikut.
(a + b)(c + d) = (a + b)c + (a + b)d
= ac + bc + ad + bd
= ac + ad + bc + bd
3. Pembagian Bentuk Aljabar
Pembagian bentuk aljabar akan lebih mudah jika dinyatakan dalam bentuk pecahan. Pelajarilah contoh soal berikut.
Contoh Soal :
Tentukan hasil pembagian berikut.
a. 8x : 4
b. 16a2b : 2ab
4. Perpangkatan Bentuk Aljabar
Di Kelas VII, kamu telah mempelajari definisi bilangan berpangkat. Pada bagian ini materi tersebut akan dikembangkan, yaitu memangkatkan bentuk aljabar.
a = bilangan rill
n = bilangan asli
Definisi bilangan berpangkat berlaku juga pada bentuk aljabar. Untuk lebih jelasnya, pelajari uraian berikut.
a. a5 = a × a × a × a × a
b. (2a)3 = 2a × 2a × 2a = (2 × 2 × 2) × (a × a × a) = 8a3
c. (–3p)4 = (–3p) × (–3p) × (–3p) × (–3p)
= ((–3) × (–3) × (–3) × (–3)) × (p × p × p × p) = 81p4
d. (4x2y)2 = (4x2y) × (4x2y) = (4 × 4) × (x2 × x2) × (y × y) = 16x4y2
Sekarang, bagaimana dengan bentuk (a + b)2?
Bentuk (a + b)2 merupakan bentuk lain dari (a + b) (a + b). Jadi, dengan menggunakan sifat distributif, bentuk (a + b)2 dapat ditulis:
(a + b)2 = (a + b) (a + b)
= (a + b)a + (a + b)b
= a2 + ab + ab + b2
= a2 + 2ab + b2
Dengan cara yang sama, bentuk (a – b)2 juga dapat ditulis sebagai: (
a – b)2 = (a – b) (a – b)
= (a – b)a + (a – b)(–b)
= a2 – ab – ab + b2
= a2 – 2ab + b2
Selanjutnya, akan diuraikan bentuk (a + b)3, sebagai berikut.
(a + b)3 = (a + b) (a + b)2
= (a + b) (a2 + 2ab + b2) (a+b)2 = a2 + 2ab + b2
= a(a2 + 2ab + b2 ) + b (a2 + 2ab + b2 ) (menggunakan cara skema)
= a3 + 2a2b + ab2 + a2b + 2ab2 + b3 (suku yang sejenis dikelompokkan)
= a3 + 2a2b + a2b + ab2 +2ab2 + b3 (operasikan suku yang sejenis)
= a3 + 3a2b + 3ab2 + b3
Untuk menguraikan bentuk aljabar (a + b)2, (a + b)3, dan (a + b)4, kamu dapat menyelesaikannya dalam waktu singkat. Akan tetapi, bagaimana dengan bentuk aljabar (a + b)5, (a + b)6, (a + b)7, dan seterusnya? Tentu saja kamu juga dapat menguraikannya, meskipun akan memerlukan waktu yang lebih lama. Untuk memudahkan penguraian perpangkatan bentuk-bentuk aljabar tersebut, kamu bisa menggunakan pola segitiga Pascal . Sekarang, perhatikan pola segitiga Pascal berikut
Sebelumnya, kamu telah mengetahui bahwa bentuk aljabar (a + b)2 dapat diuraikan menjadi a2 + 2ab + b2. Jika koefisien-koefisiennya dibandingkan dengan baris ketiga pola segitiga Pascal, hasilnya pasti sama, yaitu 1, 2, 1. Ini berarti, bentuk aljabar (a + b)2 mengikuti pola segitiga Pascal. Sekarang, perhatikan variabel pada bentuk a2 + 2ab + b2. Semakin ke kanan, pangkat a semakin berkurang (a2 kemudian a). Sebaliknya, semakin ke kanan pangkat b semakin bertambah (b kemudian b2). Jadi, dengan menggunakan pola segitiga Pascal dan aturan perpangkatan variabel, bentuk-bentuk perpangkatan suku dua (a + b)3, (a + b)4, (a + b)5, dan seterusnya dapat diuraikan sebagai berikut.
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
(a + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5 dan seterusnya.
Perpangkatan bentuk aljabar (a – b)n dengan n bilangan asli juga mengikuti pola segitiga Pascal. Akan tetapi, tanda setiap koefisiennya selalu berganti dari (+) ke (–), begitu seterusnya. Pelajarilah uraian berikut.
(a – b)2 = a2 – 2ab + b2
(a – b)3 = a3 – 3a2b + 3ab2 – b3
(a – b)4 = a4 – 4a3b + 6a2b2 – 4ab3 + b4
(a – b)5 = a5 – 5a4b + 10a3b2 – 10a2b3 + 5ab4 – b5
C. PEMFAKTORAN BENTUK ALJABAR
1. Pemfaktoran dengan sifat Distributif
Dengan sifat ini, bentuk aljabar ax + ay dapat difaktorkan menjadi a(x + y), di mana a adalah faktor persekutuan dari ax dan ay. Untuk itu, pelajarilah Contoh Soal berikut.
Contoh Soal :
Faktorkan bentuk-bentuk aljabar berikut.
a. 5ab + 10b
b. 2x – 8x2y
Jawab:
a. 5ab + 10b
Untuk memfaktorkan 5ab + 10b tentukan faktor persekutuan dari 5 dan 10,
kemudian dari ab dan b.
Faktor persekutuan dari 5 dan 10 adalah 5.
Faktor persekutuan dari ab dan b adalah b.
Jadi, 5ab + 10b difaktorkan menjadi 5b(a+ 2).
b. 2x – 8x2y
Faktor persekutuan dari 2 dan –8 adalah 2.
Faktor persekutuan dari x dan x2 y adalah x.
Jadi, 2x – 8x2y = 2x(1 – 4xy).
2. Selisih Dua Kuadrat
Perhatikan bentuk perkalian (a + b)(a – b). Bentuk ini dapat ditulis
(a + b)(a – b) = a2 – ab + ab – b2 = a2 – b2
Jadi, bentuk a2 – b2 dapat dinyatakan dalam bentuk perkalian (a + b) (a – b).
Bentuk a2 – b2 disebut selisih dua kuadrat
Contoh soal :
Faktorkan bentuk-bentuk
a. p2 – 4
b. 25x2 – y2
a. p2 – 4 = (p + 2)(p – 2)
b. 25x2 – y2 = (5x + y)(5x – y)
3. Pemfaktoran Bentuk Kuadrat
a. Pemfaktoran bentuk ax2 + bx + c dengan a = 1
Perhatikan perkalian suku dua berikut.
(x + p)(x + q) = x2 + qx + px + pq
= x2 + (p + q)x + pq
Jadi, bentuk x2 + (p + q)x + pq dapat difaktorkan menjadi (x + p) (x + q). Misalkan, x2 + (p + q)x + pq = ax2 + bx + c sehingga a = 1, b = p + q, dan c = pq.
Dari pemisalan tersebut, dapat dilihat bahwa p dan q merupakan faktor dari c. Jika p dan q dijumlahkan, hasilnya adalah b. Dengan demikian untuk memfaktorkan bentuk ax2 + bx + c dengan a = 1, tentukan dua bilangan yang merupakan faktor dari c dan apabila kedua bilangan tersebut dijumlahkan, hasilnya sama dengan b.
demikianlah materi aljabar yang bisa saya posting. untuk materi tentang aljabar yang lebih lengkapnya bisa anda download disini.
https://ity.im/9fPpz
demikianlah materi aljabar yang bisa saya posting. untuk materi tentang aljabar yang lebih lengkapnya bisa anda download disini.
https://ity.im/9fPpz








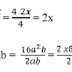


0 comments